Лабораторная работа №1.
Представление периодических импульсных
Сигналов рядом Фурье.
Цель работы – Изучение спектрального состава периодической последовательности импульсов прямоугольной формы при различных частотах следования и длительности импульсов.
Введение
Для, передачи хранения и обработки информации используются периодические импульсные сигналы, которые могут быть математически представлены рядами Фурье. Существует временное рис.1 и частотное представление электрических сигналов рис.2.
Рис.1. Временная форма представления периодической
последовательности прямоугольных импульсов.
Представление сигнала во временной области позволяет определить его параметры, энергию, мощность и длительность. Для представления сигналов в частотной области в виде спектра используется преобразования Фурье. Знание частотных свойств позволяет решать задачи идентификации характеристик сигнала (определение его наиболее информативных параметров), фильтрации (выделение полезного сигнала на фоне помех), выбора частоты дискретизации непрерывного сигнала. Одним из важнейших параметров сигнала является ширина частотного спектра, т. к. именно этот параметр оказывается определяющим при согласовании сигнала с аппаратурой обработки и передачи информации.
Основные формулы и определения.
Периодическую функциюu(t) с периодом T можно представить рядом Фурье
 (1)
(1)
Колебание ![]() с частотой называется первой гармоникой; (n =1) колебание
с частотой называется первой гармоникой; (n =1) колебание ![]() с частотой - второй гармоникой (n =2),
с частотой - второй гармоникой (n =2), ![]() c частотой - n-й гармоникой.
c частотой - n-й гармоникой.
Выражение (1) с использованием тождества
может быть переписано в виде
![]() , (2)
, (2)
![]()
![]()
Коэффициенты и определяется по формулам


Величина выражает среднее значение функции за период, она, называется также постоянной составляющей и вычисляется по формуле

Формулы (3) решают задачу анализа : по заданной периодической функции нужно найти коэффициенты Фурье и . Формулы (1) и (2) решают задачу гармонического синтеза : по заданным коэффициентам и нужно найти периодическую функцию .
Анализ спектра последовательности прямоугольных импульсов
Совокупность амплитуд и частот гармонических составляющих называютамплитудной-частотной характеристикой
(АЧХ), а зависимость от частот гармоник фазо-частотной характеристикой (ФЧХ).
Амплитудно-частотный спектр прямоугольных импульсов может быть представлен графически рис.2. 
Рис.2. АЧХ и ФЧХ периодической последовательности
прямоугольных импульсов.
Пусть , представляющая последовательность прямоугольных импульсов рис.1 с амплитудой , длительностью и периодом описывается уравнением
![]()
Тогда амплитуды и фазы для гармонических составляющих определяются уравнением:
![]() (4)
(4)
![]()
Величина называется скважностью и обозначается буквой . Тогда уравнения (4) принимают вид
![]() где n =1, 2, … . (5)
где n =1, 2, … . (5)
Для вычисления мощности сигналов представленных рядом Фурье в теории информации используют формулы в которых значение сопротивление R = 1 Ом. В этом случае напряжения u и токи i равны, поскольку i = u/R.
Мощность постоянной составляющей Р 0 будет
![]()
а мощность переменной составляющей Р n для n-й гармоники
![]() (6)
(6)
Формула для результирующей мощности примет вид

ЗАДАНИЕ
1. Выполните анализ периодической последовательности прямоугольных импульсов
1.1 По номеру варианта N, полученного у преподавателя, определите из таблицы 1 значение скважности и круговой частоты .
Таблица 1
| №, вар | q | , рад/с | №, вар | q | , рад/с |
| 3,24 | 47,25 | 8,50 | 69,22 | ||
| 6,52 | 97,50 | 6,72 | 78,59 | ||
| 5,93 | 14,45 | 2,30 | 19,44 | ||
| 7,44 | 15,12 | 3,59 | 37,96 | ||
| 1,87 | 70,93 | 4,48 | 78,27 | ||
| 5,46 | 91,65 | 2,99 | 42,48 | ||
| 6,40 | 86,40 | 6,18 | 75,45 | ||
| 1,27 | 48,98 | 1,81 | 57,64 | ||
| 2,97 | 40,13 | 3,22 | 15,46 | ||
| 1,09 | 85,95 | 3,66 | 55,25 | ||
| 2,13 | 57,30 | 3,27 | 27,58 | ||
| 7,99 | 66,90 | 4,64 | 3,68 | ||
| 4,61 | 31,55 | 3,71 | 43,73 | ||
| 1,95 | 25,24 | 4,33 | 70,44 | ||
| 2,66 | 6,61 | 3,38 | 52,07 | ||
| 1,10 | 18,37 | 6,92 | 26,17 | ||
| 4,06 | 70,24 | 4,95 | 55,52 | ||
| 2,40 | 35,10 | 6,51 | 82,64 | ||
| 9,42 | 33,96 | 3,32 | 68,07 | ||
| 6,13 | 43,25 | 7,75 | 32,49 | ||
| 7,36 | 52,37 | 5,71 | 26,68 | ||
| 2,33 | 24,84 | 2,42 | 96,02 | ||
| 2,18 | 25,34 | 16,99 | 88,59 | ||
| 5,80 | 12,99 | 62,23 | 50,21 | ||
| 1,68 | 41,16 | 37,54 | 20,70 |
1.2 а) Определите 11 первых значений коэффициентов u n (n=0, 1, 2, ... , 10), считая Е=1 В, используя электронные таблицы "Exel" (или калькулятор, или другой программный продукт) по формулам (5) и и внесите их в соответствующую строку u n таблицы 2.
1.3 б) Вычислите мощности p n и запишите их в таблицу 2.
Таблица 2
| w | w 1 | 2w 1 | … | 10w 1 | |
| u n | u 0 | u 1 | u 2 | … | u 10 |
| j n | j 1 | j 2 | j 3 | … | j 10 |
| p n | p 0 | p 1 | p 2 | p 10 |
и графика амплитудно-частотной характеристики (АЧХ) рис.3, а).
1.4 Постройте фазо-частотную характеристику (ФЧХ) периодической последовательности импульсов подобно рис.2) в которой изменение знака u n эквивалентно сдвигу фазы на p.
1.5 Вычислите удельную (на сопротивлении 1 Ом) мощность спектра первых 10 гармоник по формуле
 .
.
2. Задача синтеза.
2.1. Используя уравнение (1), представьте сумму первых 10 гармоник подставив в виде уравнения
по вычисленным в таблице значениям u n для , , , …. и постройте временную зависимость на периоде Т, например.
из таблицы 3
в виде графика 4 во временном диапазоне одного периода Т= , используя текущее время t = nD t - t/2, с шагом где n=0,1,2, … ,10 , показанного на рис. 3 .

Рис. 3. Временной интервал для синтеза сигнала
Периодические и непериодические сигналы, форма которых отличается от синусоидальной, обычно называют импульсными сигналами
. Процессы генерации, преобразования, а также вопросы практического применения импульсных сигналов относятся сегодня ко многим областям электроники.
Так, например, ни один современный блок питания не обходится без расположенного на его печатной плате генератора прямоугольных импульсов, такого например как на микросхеме TL494, выдающей импульсные последовательности с параметрами, подходящими для текущей нагрузки.

Поскольку импульсные сигналы могут иметь различную форму, то и называют различные импульсы в соответствии с похожей по форме геометрической фигурой: прямоугольные импульсы, трапецеидальные импульсы, треугольные импульсы, пилообразные импульсы, ступенчатые, и импульсы разных других форм. Между тем, наиболее часто практически применяются именно прямоугольные импульсы . О их параметрах и пойдет речь в данной статье.

Конечно, термин «прямоугольный импульс» несколько условен. В силу того что ничего идеального в природе не бывает, как не бывает и идеально прямоугольных импульсов. На самом деле реальный импульс, который принято называть прямоугольным, может иметь и колебательные выбросы (на рисунке показаны как b1 и b2), обусловленные вполне реальными емкостными и индуктивными факторами.
Выбросы эти могут, конечно, отсутствовать, однако существуют электрические и временные параметры импульсов, отражающие в числе прочего «неидеальность их прямоугольности».
Прямоугольный импульс имеет определенную полярность и рабочий уровень. Чаще всего полярность импульса положительна, поскольку подавляющее большинство цифровых микросхем питаются положительным, относительно общего провода, напряжением, и следовательно мгновенное значение напряжения в импульсе всегда больше нуля.
Но есть, например, компараторы, питаемые двухполярным напряжением, в таких схемах можно встретить разнополярные импульсы. Вообще микросхемы, питаемые напряжением отрицательной полярности, не так широко применяются, как микросхемы с обычным положительным питанием.
В последовательности импульсов рабочее напряжение импульса может принимать низкий или высокий уровень, причем один уровень с течением времени сменяет другой. Уровень низкого напряжения обозначают U0, уровень высокого U1. Наибольшее мгновенное значение напряжения в импульсе Ua или Um, относительно начального уровня, называется амплитудой импульса .

Разработчики импульсных устройств зачастую оперируют активными импульсами высокого уровня, такими как показанный на рисунке слева. Но иногда практически целесообразно применить в качестве активных импульсы низкого уровня, для которых исходное состояние - высокий уровень напряжения. Импульс низкого уровня показан на рисунке справа. Называть импульс низкого уровня «отрицательным импульсом» - безграмотно.
Перепад напряжения в прямоугольном импульсе называют фронтом, который представляет собой быстрое (соизмеримое по времени со временем протекания переходного процесса в цепи) изменение электрического состояния.
Перепад с низкого уровня к высокому уровню, то есть положительный перепад, называют передним фронтом или просто фронтом импульса. Перепад от высокого уровня к низкому, или отрицательный перепад, называют срезом, спадом или просто задним фронтом импульса.
Передний фронт обозначают в тексте 0.1 или схематически _|, а задний фронт 1.0 или схематически |_.
В зависимости от инерционных характеристик активных элементов, переходный процесс (перепад) в реальном устройстве всегда занимает некоторое конечное время. Поэтому полная длительность импульса включает в себя не только времена существования высокого и низкого уровней, но также времена длительности фронтов (фронта и среза), которые обозначаются Тф и Тср. Практически в любой конкретной схеме время фронта и спада можно увидеть при помощи .
Так как в реальности моменты начала и окончания переходных процессов в перепадах очень точно выделить непросто, то принято считать за длительность перепада промежуток времени, во время которого напряжение изменяется от 0,1Ua до 0,9Ua (фронт) или от 0,9Ua до 0,1Ua (срез). Так и крутизна фронта Кф и крутизна среза Кс.р. задаются в соответствии с данными граничными состояниями, и измеряются в вольтах в микросекунду (в/мкс). Непосредственно длительностью импульса называют промежуток времени, отсчитываемый от уровня 0,5Ua.
Когда рассматривают в общем процессы формирования и генерации импульсов, то фронт и срез принимают по длительности за ноль, поскольку для грубых расчетов эти малые временные промежутки оказываются не критичны.

Это импульсы, следующие друг за другом в определенном порядке. Если паузы между импульсами и длительности импульсов в последовательности равны между собой, то это периодическая последовательность. Период следования импульсов Т - это сумма длительности импульса и паузы между импульсами в последовательности. Частота f следования импульсов - это величина обратная периоду.

Периодические последовательности прямоугольных импульсов, кроме периода Т и частоты f, характеризуются еще парой дополнительных параметров: коэффициентом заполнения DC и скважностью Q. Коэффициент заполнения - это отношение времени длительности импульса к его периоду.
Скважность - это отношение периода импульса ко времени его длительности. Периодическая последовательность скважности Q=2, то есть такая, у которой время длительности импульса равно времени паузы между импульсами или у которой коэффициент заполнения равен DC=0,5, называется меандром.
В предыдущих разделах мы рассмотрели разложение периодических сигналов в ряд Фурье, а также изучили некоторые свойства представления периодических сигналов рядом Фурье. Мы говорили, что периодические сигналы можно представить как ряд комплексных экспонент, отстоящих друг от друга на частоту рад/c, где — период повторения сигнала. В результате мы можем трактовать представление сигнала в виде ряда комплексных гармоник как комплексный спектр сигнала. Комплексный спектр, в свою очередь, может быть разделен на амплитудный и фазовый спектры периодического сигнала.В данном разделе мы рассмотрим спектр периодической последовательности прямоугольных импульсов, как одного из важнейших сигналов, используемого в практических приложениях.
Спектр периодической последовательности прямоугольных импульсов
Пусть входной сигнал представляет собой периодическую последовательность прямоугольных импульсов амплитуды , длительности секунд следующих с периодом секунд, как это показано на рисунке 1

Рисунок 1. Периодическая последовательность прямоугольных импульсов
Единица измерения амплитуды сигнала зависит от физического процесса, который описывает сигнал . Это может быть напряжение, или, сила тока, или любая другая физическая величина со своей единицей измерения, которая меняется во времени как . При этом, единицы измерения амплитуд спектра , , будут совпадать с единицами измерения амплитуды исходного сигнала.
Тогда спектр , , данного сигнала может быть представлен как:

Спектр периодической последовательности прямоугольных импульсов представляет собой множество гармоник с огибающей вида
![]() .
.
Свойства спектра периодической последовательности прямоугольных импульсов
Рассмотрим некоторые свойства огибающей спектра периодической последовательности прямоугольных импульсов.
Постоянная составляющая огибающей может быть получена как предел:
Для раскрытия неопределенности воспользуемся правилом Лопиталя :
Где называется скважностью импульсов и задает отношение периода повторения импульсов к длительности одиночного импульса.
Таким образом, значение огибающей на нулевой частоте равно амплитуде импульса деленной на скважность. При увеличении скважности (т.е. при уменьшении длительности импульса при фиксированном периоде повторения) значение огибающей на нулевой частоте уменьшается.
Используя скважность импульсов выражение (1) можно переписать в виде:
Нули огибающей спектра последовательности прямоугольных импульсов можно получить из уравнения:

Знаменатель обращается в ноль только при , однако, как мы выяснили выше
![]() , тогда решением уравнения будет
, тогда решением уравнения будет
Тогда огибающая обращается в ноль если
На рисунке 2 показана огибающая спектра периодической последовательности прямоугольных импульсов (пунктирная линия) и частотные соотношения огибающей и дискретного спектра .

Рисунок 2. Cпектр периодической последовательности прямоугольных импульсов
Также показаны амплитудная огибающая , амплитудный спектр , а также фазовая огибающая и фазовый спектр .Из рисунка 2 можно заметить, что фазовый спектр принимает значения когда огибающая имеет отрицательные значения. Заметим, что и соответствуют одной и той же точке комплексной плоскости равной .
Пример спектра периодической последовательности прямоугольных импульсов
Пусть входной сигнал представляет собой периодическую последовательность прямоугольных импульсов амплитуды , следующих с периодом секунды и различной скважностью . На рисунке 3а показаны временные осциллограммы указанных сигналов, их амплитудные спектры (рисунок 3б), а также непрерывные огибающие спектров (пунктирная линия).

Рисунок 3. Cпектр периодической последовательности
прямоугольных импульсов при различном значении скважности
а — временные осциллограммы; б — амплитудный спектр
Как можно видеть из рисунка 3, при увеличении скважности сигнала, длительность импульсов уменьшается, огибающая спектра расширяется и уменьшается по амплитуде (пунктирная линия). В результате, в пределах главного лепестка увеличивается количество гармоник спектра .
Спектр смещенной во времени периодической последовательности прямоугольных импульсов
Выше мы подробно изучили спектр периодической последовательности прямоугольных импульсов для случая, когда исходный сигнал являлся симметричным относительно . В результате спектр такого сигнала является вещественным и задается выражением (1). Теперь мы рассмотрим, что произойдет со спектром сигнала если мы сместим сигнал во времени,как это показано на рисунке 4 .

Рисунок 4. Сдвинутая во времени периодическая последовательность прямоугольных импульсов
Смещенный сигнал можно представить как сигнал ,
задержанный на половину длительности импульса
![]() .
Спектр смещенного сигнала можно представить
согласно свойству
циклического временного сдвига
как:
.
Спектр смещенного сигнала можно представить
согласно свойству
циклического временного сдвига
как:
Таким образом, спектр периодической последовательности прямоугольных импульсов, смещенной относительно нуля, не
является чисто вещественной функцией, а приобретает дополнительный фазовый множитель
![]() .
Амплитудный и фазовый
спектры показаны на рисунке 5.
.
Амплитудный и фазовый
спектры показаны на рисунке 5.

Рисунок 5. Амплитудный и фазовый спектры сдвинутой во времени периодической последовательности прямоугольных импульсов
Из рисунка 5 следует, что сдвиг периодического сигнала во времени не изменяет амплитудный спектр сигнала, но добавляет линейную составляющую к фазовому спектру сигнала.
Выводы
В данном разделе мы получили аналитическое выражение для спектра периодической последовательности прямоугольных импульсов.
Мы рассмотрели свойства огибающей спектра периодической последовательности прямоугольных импульсов и привели примеры спектров при различном значении скважности.
Также был рассмотрен спектр при смещении во времени последовательности прямоугольных импульсов и показано, что смещение во времени изменяет фазовый спектр и не влияет на амплитудный спектр сигнала.
Москва, Советское радио, 1977, 608 c.Дёч, Г. Руководство по практическому применению преобразования Лапласа. Москва, Наука, 1965, 288 c.
В данном выражении
| |
функция sinc, как показано на рис. 2.6, достигает максимума (единицы) при у = 0и стремится к нулю при у ® ±¥, осциллируя с постепенно уменьшающейся амплитудой. Через нуль она проходит в точках у = ±1, ±2, …. На рис. 2.7, а как функция отношения п/Т 0 показан амплитудный спектр последовательности импульсов |с n |, а на рис. 2.7, б изображен фазовый спектр q n . Следует отметить, что положительные и отрицательные частоты двустороннего спектра - это полезный способ математического выражения спектра; очевидно, что в реальных условиях воспроизвести можно только положительные частоты.
Отношение
Идеальная периодическая последовательность импульсов включает все гармоники, кратные собственной частоте. В системах связи часто предполагается, что значительная часть мощности или энергии узкополосного сигнала приходится на частоты от нуля до первого нуля амплитудного спектра (рис. 2.7, а ). Таким образом, в качестве меры ширины полосы последовательности импульсов часто используется величина 1/T (где Т - длительность импульса). Отметим, что ширина полосы обратно пропорциональна длительности импульса; чем короче импульсы, тем более широкая полоса с ними связана. Отметим также, что расстояние между спектральными линиями Df = 1/Т 0 обратно пропорционально периоду импульсов; при увеличении периода линии располагаются ближе друг к другу.
Таблица 2.1. Фурье-образы
| x (t ) | X (f ) |
| d(t ) | |
| d(f ) | |
| cos 2 pf 0 t | /2 |
| sin 2 pf 0 t | /2 |
| d(t - t 0) | |
| d(f - f 0) | |
| , a >0 | |
 | |
| | |
| exp(-at )u (t ), a >0 | |
| rect(t / T ) | T sinc fT |
| W sinc Wt | rect (f / W ) |
 |
 sinc x
=
sinc x
=
Таблица 2.2 Свойства преобразования Фурье f )
Спектральное представление временных функций широко используется в теории связи. Для теоретических и экспериментальных исследований характеристик электрических цепей и передачи сообщений по каналам связи используется различные типы сигналов: гармонические колебания, уровни постоянных напряжений, последовательности прямоугольных и радиоимпульсов и т. д. Особо важную роль в теоретических исследованиях электрических цепей играют вычислительные сигналы в форме единичной функции и импульсной функции (функции Дирака). Определим спектры наиболее распространенных типовых сигналов.
11.1 Спектр последовательности прямоугольных импульсов
Пусть имеется периодическая последовательность импульсов прямоугольной формы периодом Т длительностью импульсов t и и амплитудой А. Аналитическое выражение функции , описывающей импульс на отрезке , имеет вид
 (11.1)
(11.1)
График периодической последовательности импульсов изображен на рисунке 11.1.

Рисунок 11.1
Данная функция является четной, так как ее график симметричен относительно оси ординат. Тогда коэффициенты Фурье это функции вычисляются по формулам (КФТ2), где .

Число представляет собой среднее значение функции за период и называется постоянной составляющей. Частоту называют основной, или первой гармоникой, а частоты k высшими гармониками, где k=2,3,4,…
Построим амплитудный спектр рассматриваемой последовательности прямоугольных импульсов. Так как функция периодическая, то ее амплитудный спектр является линейчатым. Обозначим через расстояние между любыми соседними гармониками. Очевидно, оно равно . Амплитуда k-ой гармоники согласно (11.2) имеет вид
 (11.3)
(11.3)
Найдем отношение между периодом Т и длительностью импульса , при котором амплитуда k-ой гармоники обращается в нуль.
А 2 ≈32В, А 3 ≈15В, А 4 ≈0, А 5 ≈6,36В, А 6 ≈10,5В, А 7 ≈6,36В, А 8 ≈0, А 9 ≈4,95В, А 10 ≈6,37В.
Полученный в результате расчета амплитудный спектр приведен на рисунке 11.2.

Рисунок 11.2
Такой спектр называют линейчатым или дискретным спектром.
Аналогично рассчитаны и построены спектры для q=8 и q=16. Они приведены на рисунках 11.3 и 11.4 соответственно.
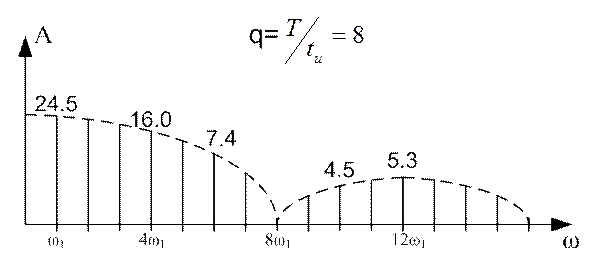
Рисунок 11.3

Рисунок 11.4
Из рисунка видно, что чем больше скважность прямоугольных импульсов, тем меньше значение имеет амплитуда первой гармоники, но тем медленнее убывает спектр.
11.2 Спектр одиночного прямоугольного импульса
Рассмотрим Ф (11.1) для случая, когда Т→∞, то есть периодическая последовательность импульсов вырождается в одиночный прямоугольный импульс, длительностью t u .
Аналитическое выражение для этого импульса запишется в виде:
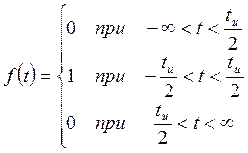
График этой функции изображен на рисунке 11.5.
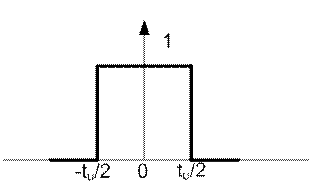
Рисунок 11.5
В этом случае частота первой гармоники и расстояние между гармониками становится равным 0, следовательно, спектр из дискретного превращается в непрерывный, состоящий из бесконечно большого числа спектральных линий, находящихся на бесконечно малых расстояниях друг от друга. Такой спектр называют сплошным. Отсюда следует важнейшее правило: периодические сигналы порождают дискретные спектры, а непериодические – сплошные (непрерывные).
Спектр прямоугольного одиночного импульса можно найти непосредственно из прямого преобразования Фурье (10.1)